De Oppervlakte van een Driehoek Berekenen
Hoe bereken je de oppervlakte van een driehoek? Deze ogenschijnlijk simpele vraag opent de deur naar een fundamenteel concept in de geometrie. Van het ontwerpen van gebouwen tot het berekenen van landareaal, de oppervlakte van een driehoek bepalen is een essentiële vaardigheid. Laten we dieper duiken in de wereld van driehoeken en hun oppervlakteberekening.
De oppervlakte van een driehoek bepalen is meer dan alleen een wiskundige oefening. Het is een praktische tool die in diverse disciplines wordt toegepast. Of je nu een student bent die worstelt met huiswerk, een architect die blauwdrukken ontwerpt, of gewoon iemand die zijn wiskundekennis wil opfrissen, het begrijpen van deze berekening is cruciaal.
Er zijn verschillende manieren om de oppervlakte van een driehoek te berekenen, afhankelijk van de beschikbare informatie. De meest bekende formule is ½ * basis * hoogte. Maar wat als je de hoogte niet kent? Geen zorgen, er zijn alternatieve methoden die we later zullen bespreken.
Het berekenen van de oppervlakte van een driehoek heeft een rijke geschiedenis, die teruggaat tot de oude Grieken. Wiskundigen zoals Euclides legden de basis voor onze huidige geometrische kennis, inclusief de formules die we vandaag de dag gebruiken.
Het belang van het kunnen berekenen van de oppervlakte van een driehoek strekt zich uit tot vele gebieden, van landmeting en engineering tot computergraphics en natuurkunde. Het is een fundamenteel concept dat ons helpt de wereld om ons heen te begrijpen en te manipuleren.
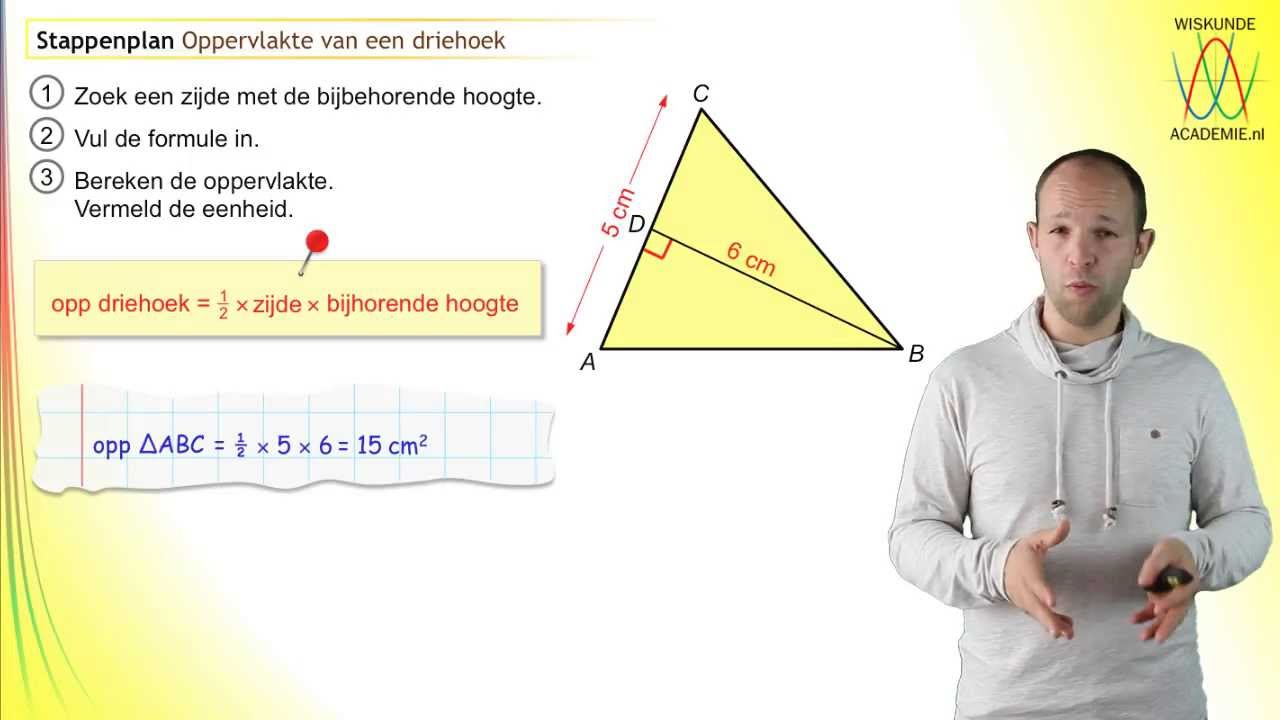
De meest gebruikte formule voor het berekenen van de oppervlakte van een driehoek is: Oppervlakte = ½ * basis * hoogte. De 'basis' is een willekeurige zijde van de driehoek, en de 'hoogte' is de loodrechte afstand van die basis tot de tegenoverliggende hoekpunt.
Voorbeeld: Een driehoek heeft een basis van 10 cm en een hoogte van 5 cm. De oppervlakte is dan ½ * 10 cm * 5 cm = 25 cm².
Een andere methode is de formule van Heron. Deze formule is handig wanneer je de lengtes van alle drie de zijden kent (a, b, c). Eerst bereken je de semiperimeter s: s = (a + b + c) / 2. Vervolgens gebruik je de formule: Oppervlakte = √(s(s-a)(s-b)(s-c)).
Voordelen van het kennen van deze berekeningen:
1. Probleemoplossing in de wiskunde: Het helpt bij het oplossen van complexere geometrische problemen.
2. Praktische toepassingen: Nuttig in beroepen zoals architectuur, engineering en landmeting.
3. Versterking van wiskundige vaardigheden: Verbetert het begrip van geometrische concepten.
Stap-voor-stap handleiding:
1. Identificeer de basis en de hoogte van de driehoek.
2. Vermenigvuldig de basis met de hoogte.
3. Deel het resultaat door 2.
Voor- en nadelen
| Voordelen | Nadelen |
|---|---|
| Eenvoudige berekening met basis en hoogte | Hoogte kan soms moeilijk te bepalen zijn |
| Veelzijdige formules beschikbaar | Heron's formule kan complex zijn voor grote getallen |
Veelgestelde vragen:
1. Wat is de basis van een driehoek? Antwoord: Een willekeurige zijde.
2. Wat is de hoogte van een driehoek? Antwoord: De loodrechte afstand van de basis tot de tegenoverliggende hoekpunt.
3. Kan ik de oppervlakte berekenen zonder de hoogte te kennen? Antwoord: Ja, met Heron's formule.
4. Wat is de eenheid van oppervlakte? Antwoord: Vierkante eenheden (cm², m², etc.).
5. Waar kan ik meer informatie vinden over driehoeken? Antwoord: Online wiskunde websites en leerboeken.
6. Hoe onthoud ik de formule voor de oppervlakte van een driehoek? Antwoord: Oefening baart kunst!
7. Wat zijn enkele praktische toepassingen van deze berekening? Antwoord: Landmeting, architectuur, engineering.
8. Hoe controleer ik of mijn berekening klopt? Antwoord: Gebruik een andere methode of een online calculator.
Tips en trucs: Teken altijd een schets van de driehoek. Label de basis en hoogte duidelijk. Gebruik een rekenmachine voor nauwkeurige berekeningen.
Conclusie: Het berekenen van de oppervlakte van een driehoek is een fundamentele vaardigheid met brede toepassingen. Van het oplossen van wiskundige problemen tot het ontwerpen van complexe structuren, het beheersen van deze berekening opent deuren naar een beter begrip van de wereld om ons heen. Door de verschillende formules en methoden te begrijpen, en door te oefenen met diverse voorbeelden, kan iedereen deze essentiële vaardigheid onder de knie krijgen. Blijf oefenen en ontdek de kracht van de driehoek!
Overwin uitstelgedrag gisteren was de makkelijkste dag
Missie naar mars wikipedia informatie
De elegante lange jurk met lange mouwen ontdek de magie